MECHANICAL MODELLING OF INTERPHASES AND INTERFACES
The crucial role of interfaces and interphases in structural problems in many areas of engineering (civil engineering, mechanical engineering, biomechanics, electronics, etc.) is now well-known. In particular, they can have a strong impact on the global response of structures subject to severe solicitations.
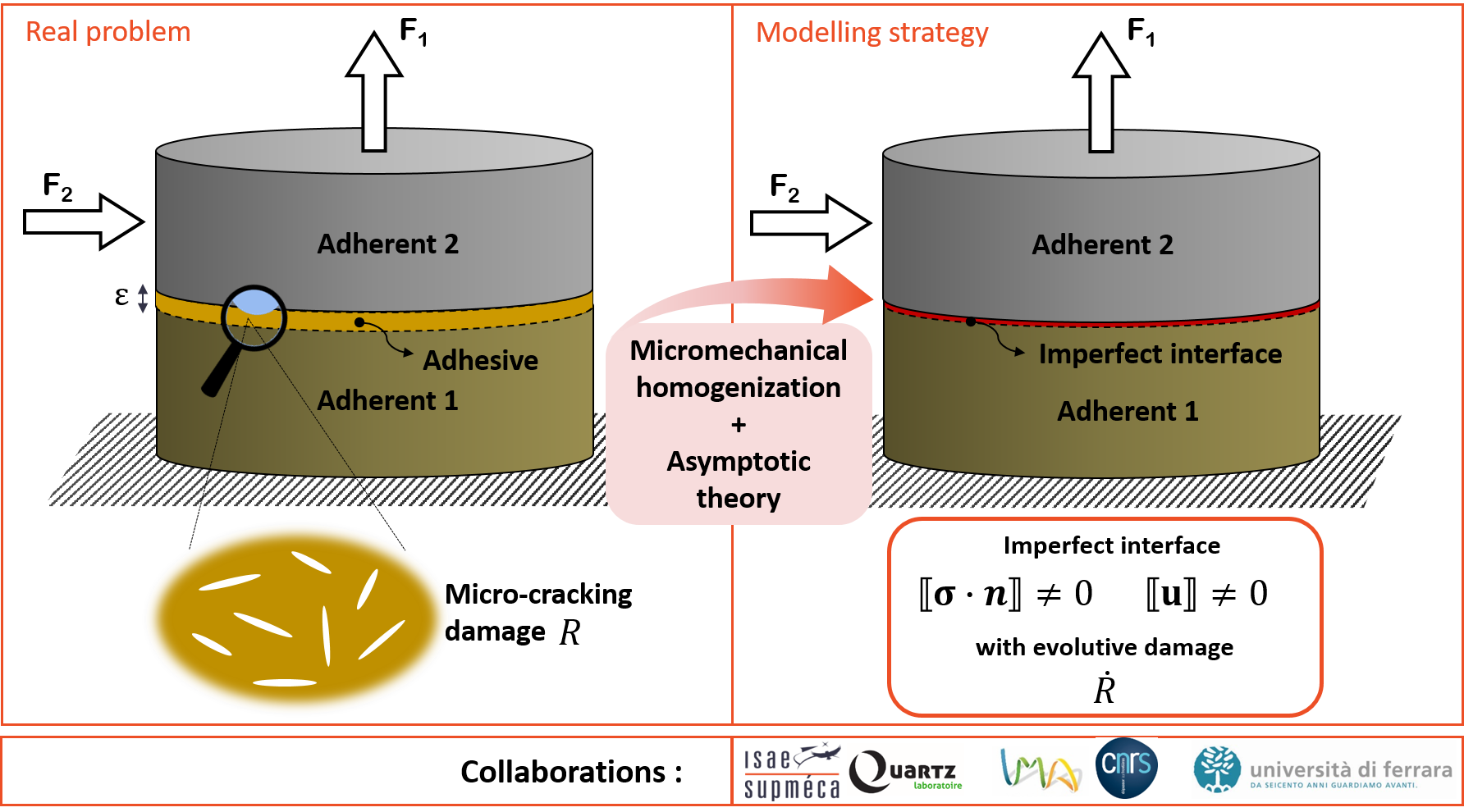
Our research works focus in a general way on the mechanical modelling of solid interphases and interfaces, that’s to say the mechanical analysis and description of phenomena deriving from the interaction between two deformable solids in the case of interfaces, and the presence of a thin layer (cf. adhesive, physico-chemical interaction zone, “third body”, etc.) between solids (cf. adherents) in the case of interphases.
Interphase/interface problems are multiscale by nature. The main purpose of studying them is often to describe microscopically (cf. the global behaviour of structures) the effects of phenomena occurring at microscopic and nanometric scale in the areas of interaction. A considerable number of scientific questions are raised and involved in particular phenomena of adhesion, friction, damage, and specific surface properties like microgeometry. Understanding these phenomena is very difficult because they occur inside the contact and do not permit direct observation. This difficulty is further compounded when dealing with problems of imperfect interfaces, that’s to say when the mechanical surfaces must accommodate relative movements and transmit efforts.
We particularly focus on soft and hard imperfect interfaces, according to the classification of the different regimes of imperfect interface according to Benveniste and Miloh [1]. Generally, the laws of imperfect interface describe the relation between the vector of interface stresses and the vector of relative movements. When continuity exists at the interface in terms of stress (i.e. no stress jump at the interface) and a discontinuity (i.e. non zero stress jump) in terms of displacements, the term soft interface (or spring-like interface) is used ; whereas the term hard interface is used when there is both a discontinuity of interface stresses and a discontinuity of relative displacements.
The main aim of our research is to develop new imperfect interface laws capable of taking into account the main physical phenomena of the contact zone or the thin layer that we want to model. To do this, a dual homogenisation is used [2] : the analytical laws governing the imperfect interface problem (interface conditions, evolution laws, etc.) are derived by applying the theory of higher order asymptotic expansions ; the effective mechanical properties of the interphase are derived through micromechanical homogenisation.
This approach has made it possible to obtain linear [2, 3] and nonlinear [4-6] imperfect interface laws that have been applied efficiently to :
- describe diffuse damage (microcracking) and its evolution in soft [7] and hard [8, 9] interfaces ;
- obtain equivalent contact stiffnesses in a rough contact problem [10] ;
- describe cohesive fracture in bonding problems [11].
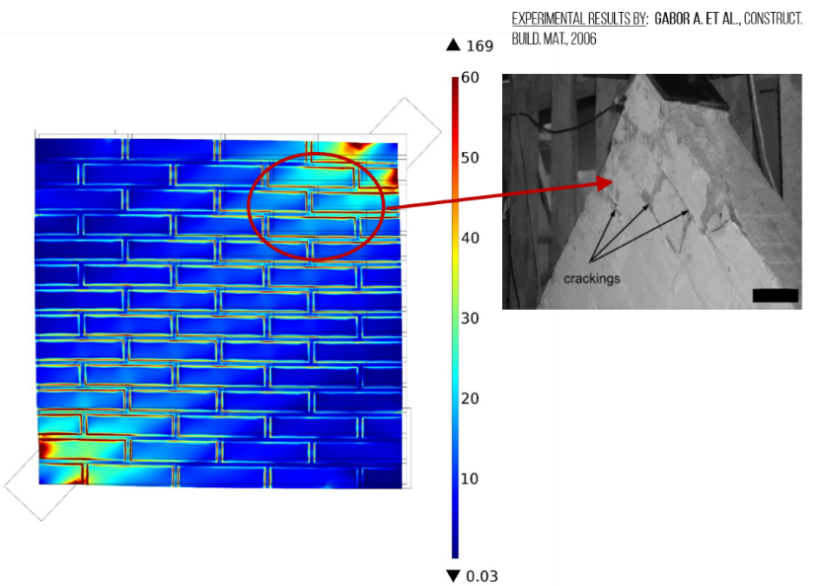
Masonry panel subjected to diagonal compression [7]. The method proposed predicts preferential microcracking zones.
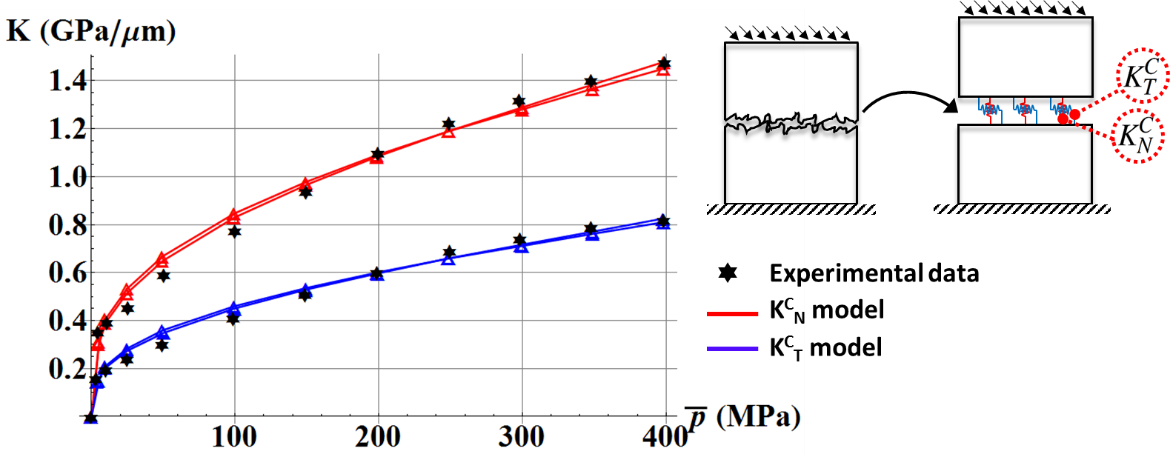
Model of a rough contact with equivalent springs [10]. Comparison of normal N and tangential T contact stiffnesses with experimental data available in the literature.
Bending test on a GFRP beam-column node [11]. Detail of the fracture of a bonded joint (left) and numerical simulation with an FE interface (right).
Collaborations
Laboratoire de Mécanique et d’Acoustique (Marseille), Université de Ferrara (Italie), Université de Salerno (Italie)
References :
- Benveniste, Y., & Miloh, T. (2001). Imperfect soft and stiff interfaces in two-dimensional elasticity. Mechanics of materials, 33(6), 309-323.
- Raffa, M. L. (2015) Micromechanical modeling of imperfect interfaces and applications. Thèse doctorale, Université de Rome “Tor Vergata” en cotutelle avec Aix-Marseille Université.
- Fouchal, F., Lebon, F., Raffa, M. L., & Vairo, G. (2014). An interface model including cracks and roughness applied to masonry. The Open Civil Engineering Journal, 8, 263-271.
- Dumont, S., Lebon, F., Raffa, M. L., & Rizzoni, R. (2017). Towards nonlinear imperfect interface models including micro-cracks and smooth roughness. Annals of Solid and Structural Mechanics, 9(1), 13-27.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2016). On modelling brick/mortar interface via a St. Venant-Kirchhoff orthotropic soft interface. Part I : theory. International Journal of Masonry Research and Innovation, 1(2), 142-164.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2018). Derivation of a model of imperfect interface with finite strains and damage by asymptotic techniques : an application to masonry structures. Meccanica, 53(7), 1645-1660.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2017). On modelling brick/mortar interface via a St. Venant-Kirchhoff orthotropic soft interface. Part II : in silico analysis. International Journal of Masonry Research and Innovation, 2(4), 259-273.
- Raffa, M. L., Rizzoni, R., & Lebon, F. (2021). A Model of Damage for Brittle and Ductile Adhesives in Glued Butt Joints. Technologies, 9(1), 19.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2022). A micromechanical model of a hard interface with micro-cracking damage. International Journal of Mechanical Sciences, 216, 106974.
- Raffa, M. L., Lebon, F., & Vairo, G. (2016). Normal and tangential stiffnesses of rough surfaces in contact via an imperfect interface model. International Journal of Solids and Structures, 87, 245-253.
- Maurel-Pantel, A., Lamberti, M., Raffa, M. L., Suarez, C., Ascione, F., & Lebon, F. (2020). Modelling of a GFRP adhesive connection by an imperfect soft interface model with initial damage. Composite Structures, 239, 112034.