Modélisation mécanique des interphases et interfaces
Le rôle crucial des interfaces et interphases dans les problèmes structuraux de nombreux domaines de l’ingénierie (génie civil, génie mécanique, biomécanique, électronique etc.) est désormais bien connu. Notamment elles peuvent fortement conditionner la réponse globale des structures sous sollicitations sévères.
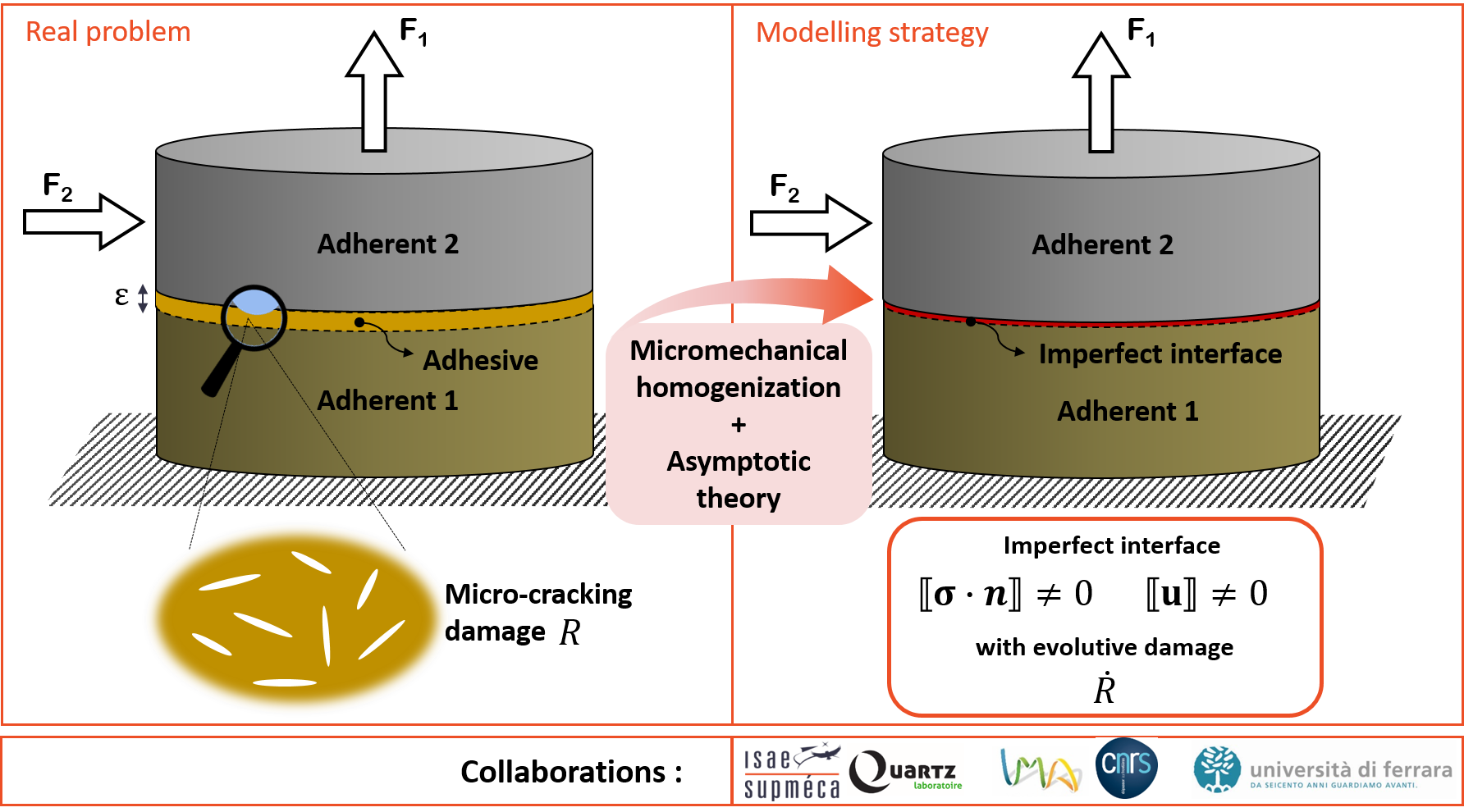
Nos travaux de recherche portent de manière générale sur la modélisation mécanique des interphases et interfaces solides, c’est-à-dire sur l’analyse et la description mécanique de phénomènes dérivant de l’interaction entre deux solides déformables dans le cas des interfaces, et de la présence d’une couche mince (cf. adhésif, zone d’interaction physico-chimique, « troisième corps », etc.) entre solides (cf. adhérents) dans le cas des interphases.
Les problèmes d’interphase/interface sont par nature, multi-échelle. Le but principal de leur étude est souvent de décrire à l’échelle macroscopique (cf. du comportement global des structures) les effets de phénomènes ayant lieu à l’échelle microscopique et nanométrique des zones d’interactions. Les questions scientifiques qui se posent sont multiples et concernent notamment les phénomènes d’adhésion, de frottement, d’endommagement, ainsi que les propriétés spécifiques des surfaces comme la microgéométrie. La compréhension de ces phénomènes est rendue particulièrement difficile lorsqu’ils se situent au sein d’un contact ne permettant pas une observation directe. Cette difficulté se trouve exacerbée lorsqu’on traite des problèmes d’interfaces imparfaites, c’est-à-dire quand les surfaces mécaniques doivent accommoder des déplacements relatifs et transmettre des efforts.
Nous nous focalisons en particulier sur les interfaces imparfaites de type soft et hard, selon la classification des différents régimes d’interface imparfaite de Benveniste et Miloh [1]. En général, les lois d’interface imparfaite décrivent la relation entre le vecteur des contraintes d’interface et le vecteur des déplacements relatifs. Lorsqu’on a une continuité à l’interface en terme de contraintes (i.e. saut nul de contraintes à l’interface) et une discontinuité (i.e. saut non nul) en termes de déplacements, on parle d’interface soft (ou interface « spring-like ») ; tandis que l’on définit une interface hard quand on a à la fois une discontinuité des contraintes d’interface et une discontinuité des déplacements relatifs.
L’objectif principal de nos recherches est de développer des nouvelles lois d’interface imparfaite capables de tenir compte des phénomènes physiques principaux de la zone de contact ou de la couche mince qu’on souhaite modéliser. Pour ce faire, une double approche d’homogénéisation est utilisée [2] : les lois analytiques régissant le problème d’interface imparfaite (conditions d’interface, lois d’évolution, etc.) sont dérivées en s’appuyant sur la théorie des développements asymptotiques à l’ordre supérieur ; les propriétés mécaniques effectives de l’interphase sont dérivées via l’homogénéisation micromécanique.
Une telle approche a permis d’obtenir des lois d’interface imparfaite linéaires [2, 3] et non-linéaires [4-6] qui ont été efficacement appliquées pour :
- décrire l’endommagement diffus (microfissuration) et son évolution dans des interfaces soft [7] et hard [8, 9] ;
- obtenir les raideurs de contact équivalentes dans un problème de contact rugueux [10] ;
- décrire la rupture cohésive dans des problèmes de collage [11].
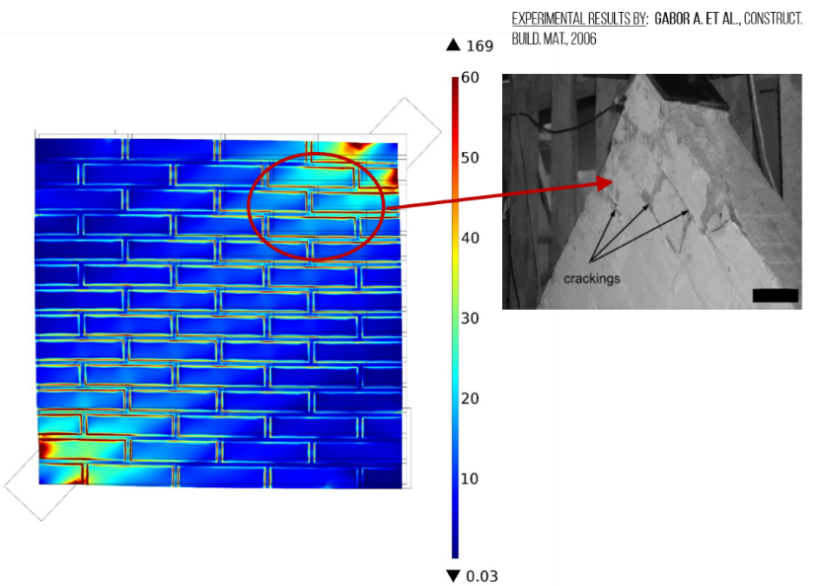
Panneau en maçonnerie soumis à compression diagonale [7]. La méthode proposée permet de prédire les zones préférentielles de microfissuration.
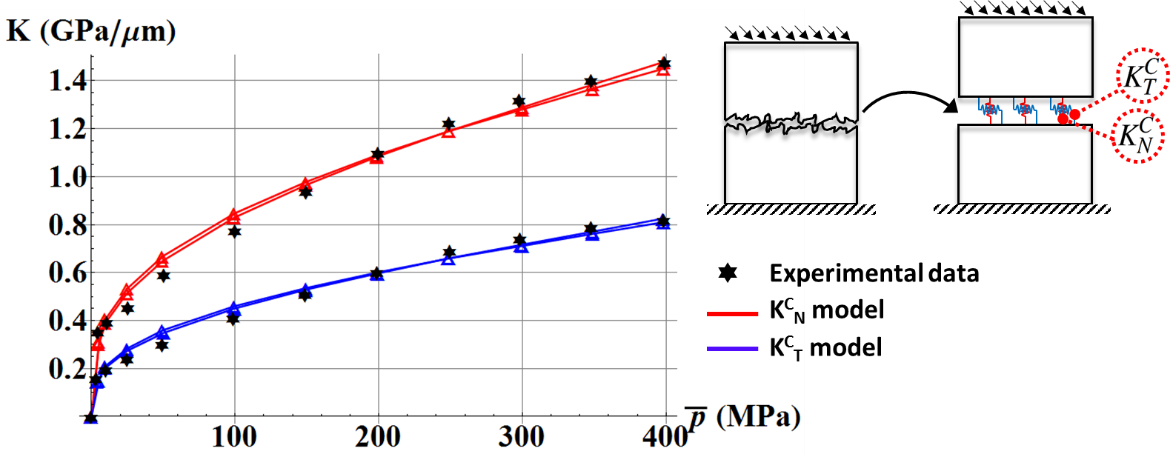
Modèle de contact rugueux à ressorts équivalents [10]. Comparaison des raideurs de contact normales N et tangentielles T avec des données expérimentales disponibles en littérature.
Test de flexion sur nœud poutre-colonne en GFRP [11]. Détail de la rupture du joint de colle (gauche) et simulation numérique avec EF d’interface (droite).
Collaborations
Laboratoire de Mécanique et d’Acoustique (Marseille), Université de Ferrara (Italie), Université de Salerno (Italie)
Références
- Benveniste, Y., & Miloh, T. (2001). Imperfect soft and stiff interfaces in two-dimensional elasticity. Mechanics of materials, 33(6), 309-323.
- Raffa, M. L. (2015) Micromechanical modeling of imperfect interfaces and applications. Thèse doctorale, Université de Rome “Tor Vergata” en cotutelle avec Aix-Marseille Université.
- Fouchal, F., Lebon, F., Raffa, M. L., & Vairo, G. (2014). An interface model including cracks and roughness applied to masonry. The Open Civil Engineering Journal, 8, 263-271.
- Dumont, S., Lebon, F., Raffa, M. L., & Rizzoni, R. (2017). Towards nonlinear imperfect interface models including micro-cracks and smooth roughness. Annals of Solid and Structural Mechanics, 9(1), 13-27.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2016). On modelling brick/mortar interface via a St. Venant-Kirchhoff orthotropic soft interface. Part I : theory. International Journal of Masonry Research and Innovation, 1(2), 142-164.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2018). Derivation of a model of imperfect interface with finite strains and damage by asymptotic techniques : an application to masonry structures. Meccanica, 53(7), 1645-1660.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2017). On modelling brick/mortar interface via a St. Venant-Kirchhoff orthotropic soft interface. Part II : in silico analysis. International Journal of Masonry Research and Innovation, 2(4), 259-273.
- Raffa, M. L., Rizzoni, R., & Lebon, F. (2021). A Model of Damage for Brittle and Ductile Adhesives in Glued Butt Joints. Technologies, 9(1), 19.
- Raffa, M. L., Lebon, F., & Rizzoni, R. (2022). A micromechanical model of a hard interface with micro-cracking damage. International Journal of Mechanical Sciences, 216, 106974.
- Raffa, M. L., Lebon, F., & Vairo, G. (2016). Normal and tangential stiffnesses of rough surfaces in contact via an imperfect interface model. International Journal of Solids and Structures, 87, 245-253.
- Maurel-Pantel, A., Lamberti, M., Raffa, M. L., Suarez, C., Ascione, F., & Lebon, F. (2020). Modelling of a GFRP adhesive connection by an imperfect soft interface model with initial damage. Composite Structures, 239, 112034.